Understanding how the circle of fifths works on guitar is vital to understanding the bigger picture of guitar music theory.
It’s the backbone of so much of the repertoire we play on a daily basis, and understanding it is vital to your development as a guitarist.
If you’d like to see the lesson this blog post is based on, click here to watch it for free — otherwise, read on!
The Circle of Fifths: Overview
Let’s return to “Happy Birthday,” this time with the knowledge that it begins on scale degree 4. Those first notes, C-D-E-F, form the last four notes of the F major scale. Are they also a part of another major scale?
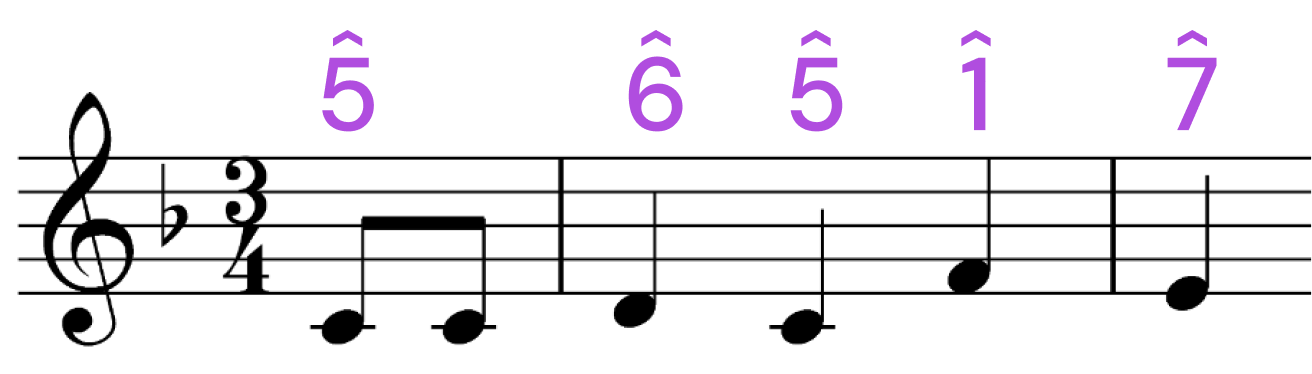
It turns out that these four notes are also the first four notes of a C major scale! This isn’t just a coincidence; let’s examine why and how.
A four-note segment of a scale is also called a tetrachord. In a major scale, we talk about the first four notes and last four notes as two different tetrachords, each spanning two whole steps and a half step.
{{trip-wire}}
Look again at the interval pattern of any major scale, and you’ll see that there actually is one repeating unit:

Scale degrees 1-4 form the first tetrachord, while scale degrees 5-8 form the second one, and they are separated by a whole step. The first part of “Happy Birthday” uses the top tetrachord of an F major scale, which is the same as the bottom tetrachord of a C major scale.
Check out Invention No. 1 by J.S. Bach.
He outlines the first tetrachord, and then catapults upward to the second tetrachord on scale degree 5. In the second bar, he takes the whole melody up five notes (also called a fifth), but leaves all the intervals intact! He essentially repeats the tune in the top tetrachord.

Just as C-D-E-F is shared by both F and C major scales, the tetrachord G-A-B-C is shared by both C and G major scales.
This makes sense, because C is a fifth above F (five notes of a scale, or five spaces and lines on a staff), and G is a fifth above C. Keys separated by a fifth will always share one tetrachord:
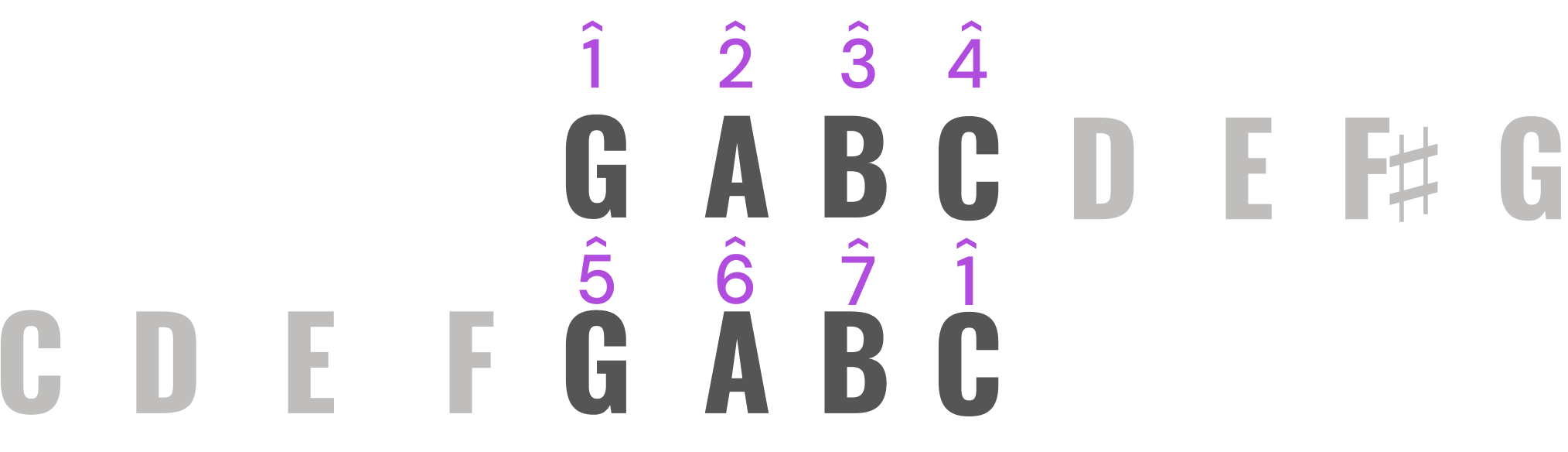
If we extend this pattern and begin Bach’s Invention No. 1 in the key of G major, then D-E-F♯ is the top tetrachord.
In which key is it the bottom tetrachord?
That would be D major – the key a fifth above G. Look at the three tetrachords that we’ve examined thus far: C-D-E-F, G-A-B-C, and D-E-F♯-G.
Each is separated by a whole step, like the mortar between bricks. The F♯ is born from the repetition of this WWH pattern.

We cannot think of musical keys as separate islands that have nothing in common.
They are in fact part of the same body of water. Notice that these new accidentals fall in a specific place within each scale: F♯ appeared as scale degree 7 in G major.
If we look at F major (the key a fifth below C), we find that B♭ appears as scale degree 4. 7 is the half step below 1, while 4 is a half step above 3.

When we move key centers by a fifth, as we just did, we introduce two new terms.
First is dominant, meaning to move upward to the fifth scale degree of any key. Its mirror image is 1 down to 4 (covering the interval of a fifth in the other direction,) which is called the subdominant.
Next, we will shift keys by moving in the dominant or subdominant direction with this motif from the Bach Invention.
If we continue to transpose this opening melody up a fifth, starting on C, we begin adding accidentals. G major births F♯, D major creates C♯, and then G♯, D♯, A♯, E♯ (yes it’s a white key, the same as F!), and finally B♯ in C♯ major, exhausting all of the options for sharps. This makes sense, because C♯ major is just C major with all the notes raised a half-step.
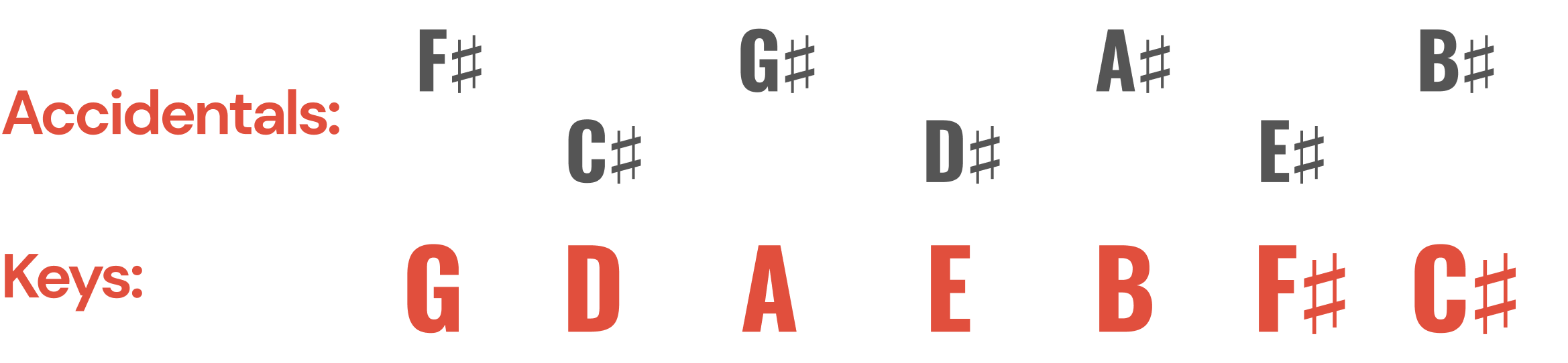
Let’s take the first four notes of this melody (CDEF), ending on scale degree 4, and begin it on scale degree 1 of the key in the subdominant direction (which is F, the same as where we left off).
Scale degree 4 in F is B♭. In B♭ major we generate an E♭, continuing to A♭, D♭, G♭, C♭, and F♭, before we’ve exhausted all the seven possble white keys that we can flat.

Through this process, we’ve created all the major and minor keys, treating C major as the center piece.
As we went, we added sharps or flats and retained them throughout the cycle. Once we added F♯, all the remaining sharp keys contained an F♯. Similarly, once we added B♭, all the remaining flat keys had one.
The flats and sharps were also generated in a very specific order. The first sharp that we added, moving up a fifth from C to G, was F♯, and so on, until we got to B♯. With flats, we began with B♭, moving down a fifth from C to F, until we got to F♭.
It’s important to remember this order, since composers use it in something called a key signature to make it easy to read lots of sharps or flats in a piece.

A shortcut for deducing key signatures: the last sharp in any key signature is also the leading tone of the major key that you’re in.
This should make sense, because scale degree 7 is always the most recent accidental generated by moving up in fifths. For flats, the second-to-last flat is the key that you’re in. In B♭ major, the flats are B and E, B♭ being the second-to-last.
Also note that most sharp keys begin on a natural note and most flat keys begin on a flat note.
We could’ve continued to F♭ major or G♯ major, but these aren’t useful as keys since they require double-sharps and double-flats to spell out the related scales.
Essentially, we’ve constructed a number line with sharps on one side and flats on the other side. How can we connect the ends of this line to create a circle?
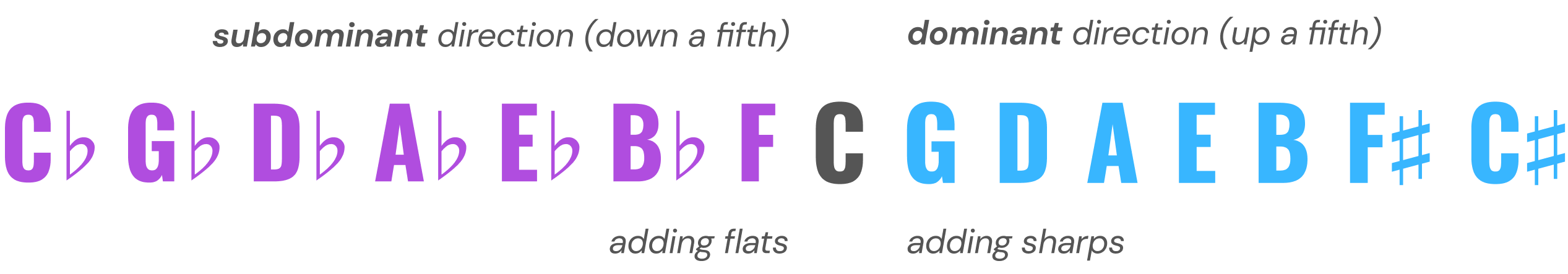
Let’s introduce a concept called enharmonic equivalence.
This says that F♯ and G♭ are fundamentally the same sound, as are the sharp and flat spellings of any black key on the keyboard. This means that we can connect the circle by saying that F♯ major (with 6 sharps) and G♭ major (with 6 flats) are really the same key.
Play these two scales on the keyboard and you’ll see they use the exact same pitches, just spelled differently. What’s even more fascinating is that we derived these scales by going in different directions from C: F♯ by moving toward the dominant, and G♭ by moving toward the subdominant.

Similarly, B major can also be called C♭ major, and C♯ major can also be D♭ major. Our number line has 15 keys, of which only 12 contain unique sets of pitches. The remaining 3 are enharmonically equivalent to another key.
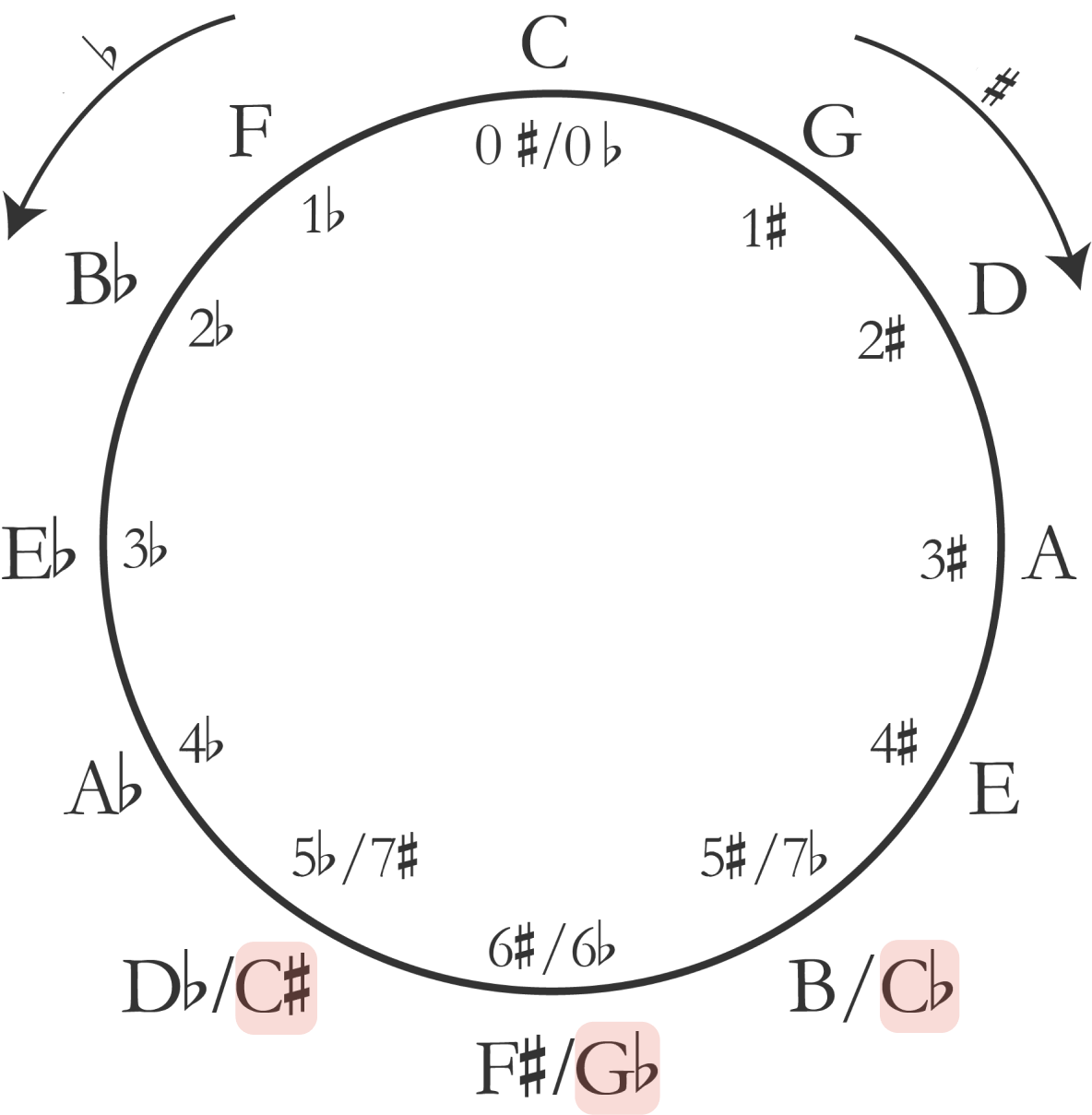
If we can derive the minor mode from a major scale, then surely all the key signatures will also apply to the relative minors.
Remember that the sixth scale degree of any major key is its relative minor (we can also count two steps backward from the root to get t the same note!) Before going to the next page, try to figure out the relative minor keys of all 12 major keys above on the now-completed circle of fifths.

Every key has a set of 5 other closely related major and minor keys. Closely related keys are defined as those with only one accidental different from a central key. We’ll explore this concept in further detail in a later lesson.
Note that the same phenomenon of enharmonic equivalence applies to minor keys. E♭ and D♯ minor have the same sound, and we can find examples from the repertoire in both keys. Seeing seven sharps or flats is quite rare but it can happen, such as in Beethoven’s Op. 26 sonata in A♭ minor, or Bach’s Prelude and Fugue in C♯ major.
The best way to internalize this circle of fifths is not by staring at it intently, but by playing music in all these keys!
Take Mozart’s “Eine Kleine Nachtmusik” and play the opening motif at a keyboard in the key of C. Notice that the note you end on is the fifth of the key.
Treat that as the new 1 and play the motif in that new key. Repeat this in all sharp and flat keys. Shift octaves if you end up too low or too high.
For minor keys, let’s play the opening melody of Paganini’s Caprice No. 24 for Violin. This melody begins by outlining scale degrees 1-2-3 of minor, and then uses the raised 6th and 7th from melodic minor. Play this melody through all the sharp and flat keys.

If you’re looking for even more practice, try the major scale in all 12 keys, beginning in C, and then starting on C♯, then D, D♯, etc. until you’re back at C. Rising by half step results in a zig-zag pattern across the circle of fifths.
Circle of fifths on guitar
Not all keys are created equal on the guitar!
Modern-day guitars are usually tuned in E, meaning they’re especially well-suited to music in E major (despite containing four sharps and being not that friendly to read for pianists).
This is because the guitar’s open strings are E, A, D, G, B, and E. Open strings sound louder, more resonant, and are easier to physically play. Four of our six open strings form an E minor chord by themselves.
The keys of A and G are also guitar-friendly because of the open Es, G, A, and D. D major and D minor work great, especially if the sixth string is tuned down to low D (this is the most common tuning alternative).
C major is pretty good because of the Es and G. C minor is actually not friendly because the open Es are not compatible with that key. F major and E♭ major are also not too well-suited for the instrument.
For example, playing an F major chord requires a barre on the first fret, which is where the strings need the most tension. Keys in these more difficult keys will usually sound quiet and shy because it’s much harder to play them loudly.

Conclusion
As you can see, the circle of fifths exists in almost every piece of music we encounter. Its inner workings allow for all of the music we enjoy to sound and function as it does.
If you’d like to watch the lesson on this topic for free, just click here.
Ready to learn more about classical guitar music theory and make real progress in your classical guitar studies?
Click below to start your tonebase membership with a 14-day free trial. By doing so, you’ll unlock complete access to 100s of premium classical guitar lessons and structured courses, along with:
- LIVE workshops with top artists and pedagogues every week
- The active tonebase Community where you can give and get feedback, and participate in skill-building Challenges and Two-Week Intensives
- Hundreds of enriched workbooks, annotated scores and other digital resources to aid you in your learning
To unlock access to it all, and open up a new door to mastery and confidence on the guitar, become a tonebase member today.

























































